Paper Reading: Pushdown Layers

2025-03-14

8 min read

Paper Reading

2025 Paper Reading

The paper reading note for Pushdown Layers, the project site of which is Pushdown Layers.

!! Still Under Construction

General

在 Autoregressive 更新的时候，Pushdown Layers 这个架构相比普通 Vanilla Transformer 维护一个 stack tape，相当于维护一个partial parse。这样在结束一个句子生成之后，其成分文法的解析(Constituency Parse)也会同时生成完毕；并且其可以获得语法信息，因此可以获得更高的 perf.

在架构中，除了标准注意力机制外，有一个 附属头 attachment head 专门预测 $r_k$，每次生成新token $k$ 之后，$k$ 应该与哪个成分节点进行归约(reduce, reduction)（然后 shift），抑或是直接 shift。归约指的是当前的 $x_k$ token 和之前某个成分进行迭代性的结合（也就是从 $k$ 到 $r_k$ 一步步地结合回去，每一步都是成分节点的结合），称为 $x_k$ reduce with the constituent to which $x_{r_k}$ belongs.

我们同时维护一个 stack tape 来记录每一步下的 partial parse 的嵌套深度信息。

注：在这篇论文中，我们的下标是从 $k=1$ 开始的。

Parallelism in Training

架构仍然允许训练并行化，因为我们仅仅多了一层无依赖关系的 $r_k$ 的 label 需要判断loss，以及原有的 AR loss，也就是说我们并不需要在训练的时候真的 update stack tape/partial parse，故训练中并不会有前后 token 的依赖关系。

Stack Tape

在 PL （的推理过程）中，我们维护一个 “stack tape” $\cal W$，相当于一条随着当前解码而增加长度的纸带（数组），每一个元素对应相应 token 在目前的 partial parse 中的嵌套深度。第 $k$ 步的stack tape是$\mathcal W_k$.

注意我们设 $\mathcal W_k,,\forall k$ 的长度是全句长度 $n$，初始化：$\mathcal W_1 = [0,0,\dots,0]$

$\mathcal W$ 的内容，也即各 token 在某步的嵌套深度，作为 embeds 被加入为 (token) attention 的额外信息。注意在真正的推理中，对第 $k$ 步，我们有 $\mathcal W_k$ 作为这个 array of depths，因此我们可以把每一步的 $\mathcal W_k$ 全都收集起来，如 causal mask 状地在训练中矩阵化、且并行化使用。

Partial Parse $\approx$ Stack of constituents

推理时，我们确实会维护一个 partial parse，通过 stack 的方式。这个 stack 的结构是，保持序列中 token 顺序，并且包含各个当前步可以访问并 reduce 到的成分。从初始到句子 parse - 生成结束，这个 stack 会一直更新。

Stack Tape Update (Partial Parse Update)

General Update Rule

每当模型预测出一个 token $x_k$ 后，在预测再下一个词之前，会通过 attachment head 决定 selected token = attached token，由此决定当前 token 是否与前面的成分进行归约（reduce，此时 $r_k<k$）再 shift，或者仅仅以 shift 的方式独立进入栈中（此时 $r_k=k$）。这种决策是基于预测出的 $r_k$ 的。这种决策使得模型能够在生成文本的同时构建出递归结构的二叉解析树。

设 $r_k$ 为每个成分节点对应的子序列的最右元素(rightmost element)，则我们会发现如果 $r_k$ 被预测为非某成分最右的元素，那么其是非法的。基于一个（估计的）概率分布，我们建模 $r_k$ 为： $$ r_k=\arg\max_j p(j,|,x_{<k},\mathcal W_{k-1}) $$ 其中

$p$ 是 attachment head 试图模拟的分布
$x_{<k}$ 是前缀 tokens
${\cal W}_{k-1}$ 是在 $k-1$ 步的 stack tape

这一步 update，我们先初始化：

stack_tape: W_k = W_k-1
constituent = [k]

Case 1: Only Shift

当我们获取 $r_k$ 之后，如果 $r_k=k$，说明我们不需要归约，因为 attachment 是 $x_k$ 自己。这时，我们把它加进 partial parse 中，其深度为 0，因此更新 $\mathcal W_k[k]=0$，$\mathcal W_k[1,\dots,k-1]=\mathcal W_{k-1}[1,\dots,k-1]$.

if r_k == k then
	stack.push(constituent) // 更新 partial parse: 新加一个 0-depth 的纯 token
	return // only shift
end if

Case 2: Shift + Reduce

如果 $r_k<k$，说明 $x_{r_k}$ 所在的成分节点（对应的子树）要和 $x_k$ 进行结合，生成新的成分节点。这个结合可能中间跨了一些其他成分，因此需要一路结合回去。所以此处有一个 while loop 来说明一切，注意：我们让 $r_k$ 作为 rightmost element 的 index：

while true do:
	top = stack.pop() // top 是某个位置=token pos，对应了某个token
	
	// perform a reduce
	// 并非是直接生成list，而是成为了node，需要用这个抽象化之后的node继续做结合
	// 另外，constituent的元素都应该是token pos(index)而不是它们本身
	constituent = (top + constituent).nodeify() 
	
	// update depths in stack tape
	for all d in constituent do:
		// 因为抽象化成node，故成分中的所有[叶子 leaves as tokens]都需要加一层depth
		stack_tape: W_k[d] += 1 
	end for
	
	if top == r_k then:
		break // 不再继续reduce
	end if
end while
stack.push(constituent) // 更新 partial parse: 结合了一堆，某些token删出去再和 x_k 以同一个成分的身份加进来

Example 1

我们可以举一个简单的例子，帮助说明这个过程：

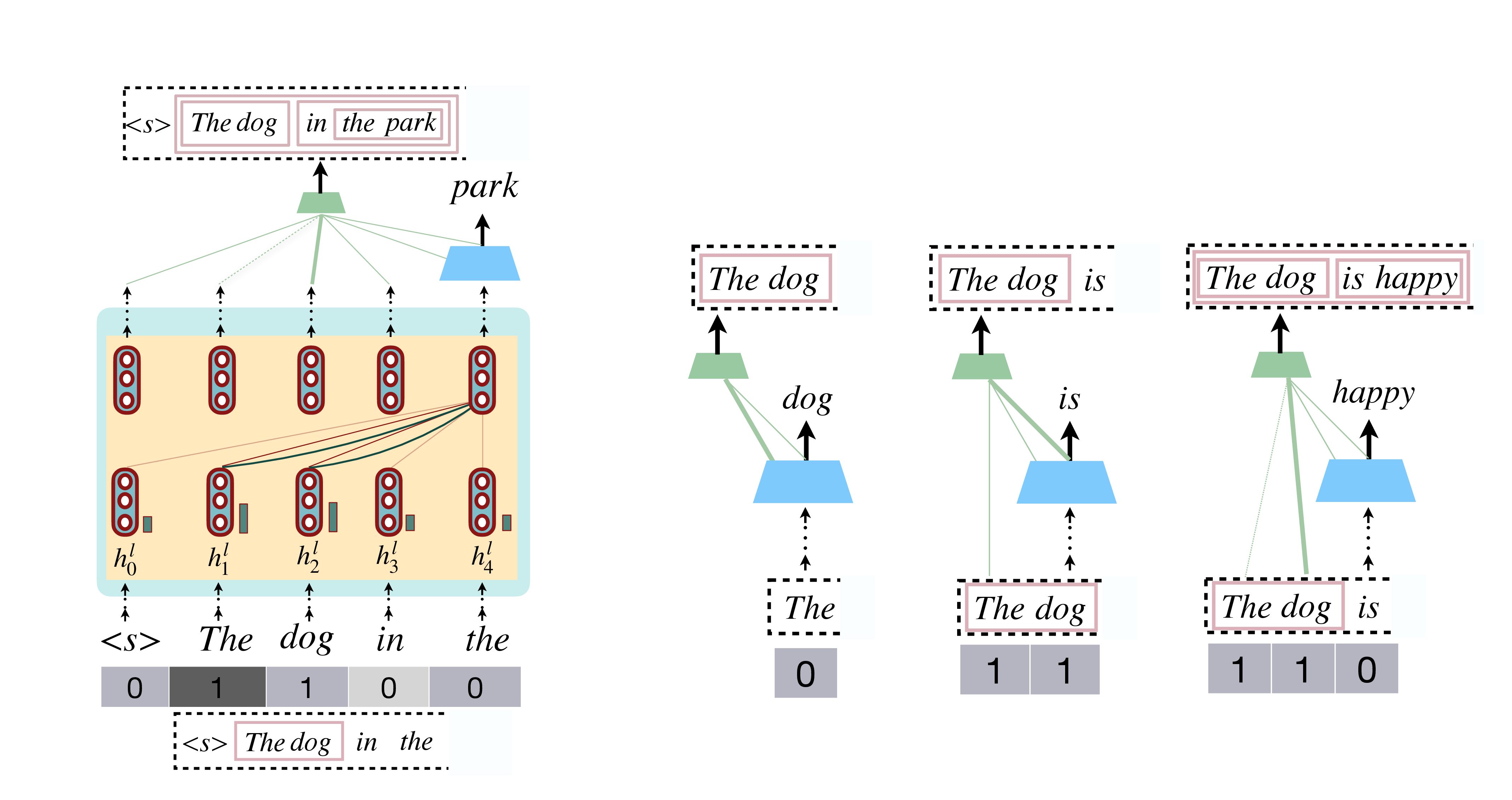
假设输入句子是 “The dog is happy”。在模型逐步生成句子时，会执行以下步骤：

预测 “The” 初始时栈带中没有任何归约信息，所以当模型预测出 “The” 时，默认执行 shift 操作，即直接将 “The” 加入栈中，赋予深度 0。
预测 “dog” 当预测出 “dog” 后，模型会同时计算一个附件得分，用来判断是否对当前栈中的已有 token 进行归约。
- 如果选择 shift，那么 “dog” 会单独以深度 0 加入栈。
- 如果选择 reduce，模型就会将 “dog” 与栈中之前的 token（例如 “The”）归约在一起，形成一个新的语法成分，并将这些 token 的深度增加（例如从 0 增加到 1）。
假设这里模型选择了 reduce 操作，那么 “The” 和 “dog” 被归约成一个成分，即形成部分解析树 [The dog]，对应的栈带会更新为 [1, 1]。
预测 “is” 接下来，模型预测 “is”，此时可能没有合适的归约目标，所以通常选择 shift 操作，将 “is” 以深度 0 加入栈中。栈带可能变为 [1, 1, 0]。
预测 “happy” 最后，当预测 “happy” 时，模型再次计算附件得分，决定是否对当前栈中的某个成分执行 reduce。假设模型判断 “happy” 应该与前面的成分 [The dog] 进行归约，则执行 reduce 操作：
- 模型选择归约的目标 token，例如选定归约目标为 “dog”（即归约整个成分 [The dog]），
- 将 “happy” 与该成分归约，更新整个成分中所有 token 的深度（例如从 1 更新为 2），
- 此时，归约后的解析树变为 [[The dog] [is happy]]，栈带更新为 [2, 2, 2, 2]。

Example 2: The dog is -> happy

我们以“[1, 1, 0]”为例来详细说明在预测出“happy”之后的归约决策过程。这里的“[1, 1, 0]”表示当前前三个token的深度：

“The” 的深度为 1
“dog” 的深度为 1（这说明之前模型已经将“The”和“dog”归约成了一个成分，即 [The dog]）
“is” 的深度为 0（还未参与归约）

当模型预测出下一个token “happy” 时，会同时计算一个附件得分，用以决定是直接将“happy”以shift操作入栈，还是与前面的成分归约（reduce）。假设附件头计算后选择的归约候选是“dog”所在的成分，也就是 [The dog]，并且 $r_k=2$，那么归约操作的详细步骤如下（参见论文中的 Algorithm 1）：

初始化：
- 令当前token的索引为 k（此时 k 对应 “happy”）。
- 定义一个初始的局部成分：constituent = [k]，也就是 [happy]。
判断是否直接 shift：
- 如果选定的归约候选 $r_k$ 等于 $k$，则说明模型决定不做归约，只是简单地 shift（即直接将“happy”入栈，深度保持为 0）。
- 但在这里 $r_k\ne k$（$r_k=2$ 对应的是 [The dog]，具体说是选定了“dog”所在的成分），因此进入归约（reduce）的循环。
归约循环：
- 第一次循环：
  - 从栈中弹出最顶层的成分。假设栈顶元素是 [is]（对应token “is”，它当前的深度为 0）。
  - 将这个弹出的成分与当前的 constituent 合并，更新为： constituent = [is] + [happy] = [is, happy]。此时需要注意，这个成分成为了一个 parent 指向两个 child 的 parent，而非是这个 list 本身。接下来我们要拿这单个抽象的node作为"一个token"来继续结合
  - 对 constituent 中所有 token 的深度进行更新：
    - “is”的深度从 0 增加 1，变为 1；
    - “happy”从初始（可以视为 0 或刚刚加入时的状态）增加 1，变为 1。
  - 检查：若刚弹出的成分 [is]与选定的归约候选不匹配，则继续下一轮。这里 [is] 与 $r_k$（[The dog]）不匹配，所以继续。
- 第二次循环：
  - 再次从栈中弹出下一个成分。此时弹出的成分为 [The, dog]（即之前通过 reduce 得到的成分，对应于 $r_k$）。
  - 将这个成分与当前的 constituent 合并： constituent = [The, dog] + [is, happy] = [[The dog], [is happy]]
  - 对 constituent 中所有 token 的深度再一次更新（将它们的深度都增加 1）：
    - “The”和“dog”原本的深度从 1 增加到 2；
    - “is”从刚才更新后的 1 增加到 2；
    - “happy”从 1 增加到 2。
  - 检查：此时弹出的成分 [The, dog]正好与选定的归约候选 $r_k$ 匹配，因此退出循环。
结束归约并更新栈：
- 将合并后的新成分 [The, dog, is, happy] 推入栈中。
- 同时，栈带中的深度信息也被更新为 [2, 2, 2, 2]，反映出所有这些 token 现在都处于同一更高层次的成分中。
- 最终，这个归约过程构建了一个解析结构，可以理解为将原来的成分 [The dog] 与后面的 [is happy] 组合起来，形成了解析树 [[The dog] [is happy]]。

补充说明： 每个token在预测后都会进行类似的决策：

如果模型判断当前token不需要与之前的成分合并，就执行 shift 操作，让它独自入栈，保持深度为 0；
如果需要与之前的成分归约，就依据附件头计算的概率，选择一个候选成分（如本例中的 [The dog]），然后通过上面的归约步骤更新栈带和构建新的语法成分。

这样，模型在生成序列的同时，就可以逐步构建出反映递归句法结构的二叉解析树。