INFOTH Note 3: Relative Ent. (KL), Mutual Info.
I now start cancel numbering for sections since I’m lazy.
3.1 Log-sum Inequality
Theorem
Suppose $a_i,b_i>0$ for a countable set $\mathcal X$, then
$$ \sum_{i\in\mathcal X}a_i\log {a_i\over b_i}\ge a\log b,\quad a=\sum_i a_i, \quad b=\sum_i b_i. $$Proof
Using Jensen’s Inequality, given $u\log u$ is convex and $\sum_i (b_i/b) = 1$
$$ \begin{aligned} \sum_{i\in\cal X}a_i\log {a_i\over b_i}&=b\sum_{i}({b_i\over b}){a_i\over b_i}\log {a_i\over b_i} \\&= b\sum_i \lambda_i u_i\log u_i,\qquad\lambda_i:=b_i/b,\quad\sum_i\lambda_i=1,\quad u_i=a_i/b_i, \\&\ge b\cdot (\sum_i\lambda_iu_i) \cdot \log \sum_i\lambda_iu_i \\&=b\cdot(\sum_i{a_i\over b})\cdot\log \sum_i {a_i\over b} \\&=a\log{a\over b}.\qquad\square \end{aligned} $$3.2 Relative Entropy (KL distance)
Def: Relative Entropy 相对熵 = KL散度
The relative entropy i.e. Kullback-Leibler (KL) Distance between 2 probability mass functions $p(x)$ and $q(x)$ is defined as
$$ D(p||q)=\sum_{x\in\mathcal X}p(x)\log{p(x)\over q(x)}\equiv E_p[\log{p(X)\over q(X)}] $$Def: Cross Entropy
$$ H(p||q)=\sum_x p(x)\log q(x)=E_p[\log q(X)] $$When we are predicting the labels (one-hots) $p$ with $p'$ we have the $H(p||p')$ as the loss.
And the relation of KL, cross entropy and entropy is
$$ H(p) = H(p||q) + D(p||q) $$Properties of KL
-
Asymmetric: $D(p||q)\ne D(q||p)$ in general.
For example, $p=(1/2,1/2)$ and $q=(1,0)$. Both on the alphabet ${\cal X}=\{0,1\}$.
Then
- $D(q||p)=1\cdot \log2 + 0=1$, while $D(p||q)=\frac12\log(\frac12/0)+\frac12\log(\frac12/1)=+\infty$
We can observe the image space of $D$.
$D:\Delta_{\cal X}\times \Delta_{\cal X}\mapsto \R\cup \{+\infty\}$
-
Nonnegative: $D(p||q)\ge 0$ always, where $D(p||q)=0\iff p=q$
-
Jointly Convex, for the pair $(p,q)$.
For $\forall t\in[0,1]$,
$$ D(tp_1+(1-t)p_2||tq_1+(1-t)q_2)\le tD(p_1||q_1)+(1-t)D(p_2||q_2). $$
3.3 Mutual Information
Def: Mutual Info.
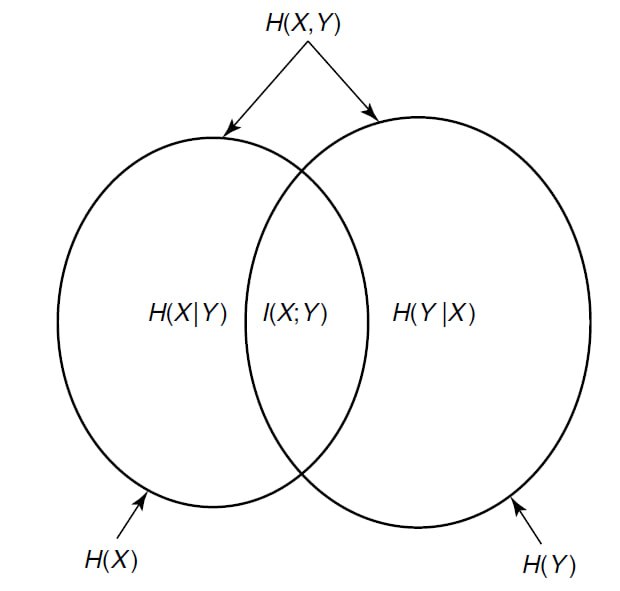
$$ I(X;Y)=I(Y;X)=D(\Pr(X,Y)||\Pr(X)\Pr(Y))=H(X)-H(X|Y)=H(Y)-H(Y|X) $$Break the KL Divergence down, for discrete distributions of $X$ and $Y$ named $p_X$ and $p_Y$, and their joint dist. $p_{X,Y}$:
$$ \begin{aligned} D(p_{X,Y}||p_Xp_Y) &=\sum_{x,y}p_{X,Y}(x,y)\log{p_{X,Y}(x,y)\over p_X(x) p_Y(y)} \\ & = E_{X,Y}[p_{X,Y}\log(p_{X,Y}/p_Xp_Y)] \end{aligned} $$- Memorize: Joint || Product distribution
Properties
Nonnegativity
- $I(X;Y)\ge 0$, with equality iff $X\perp\!\!\!\perp Y$ (since mutual information can be written as KL, and this KL=0 iff joint distribution equals the product distribution, which means the independence)
- equivalent to this: $H(X)\ge H(X|Y)$ or $H(Y)\ge H(Y|X)$ and the equality holds iff they are independent
- $H(X_1\dots X_n)\le \sum_i H(X_i)$; the equality of which holds iff they are mutually independent (all independent) not pairwise
- $X_j\perp\!\!\!\perp(X_1\cdots X_{j-1})$
Symmetry
$I(X;Y)=I(Y;X)$
Def: Multivariant Mutual Information
$$ I(X;Y,Z)=H(X)-H(X|Y,Z)=H(Y,Z)-H(Y,Z|X) $$Venn Diagram about Mutual Information