morphtitle

Programming Project #3 (`proj3`)

COMPSCI 180 Intro to Computer Vision and Computational Photography

Chuyan Zhou

This webpage uses the Typora Newsprint theme of markdown files.

Part 1: Defining Correspondences

We first crop the size of two images to the same. And then we use the website here to get the correspondence point pairs. There are 48 pairs of points in total.

We add four corners of the image to the correspondence point pairs. So there are 52 pairs of points in total.

My friend Junye's face with correspondence points

Now that we have got the correspondence point pairs, we create a mean set of points by averaging the x and y coordinates of the correspondence point pairs.

Then, we create a Delaunay triangulation of the mean set of points. The triangulation should be in the form of a list of connected points.

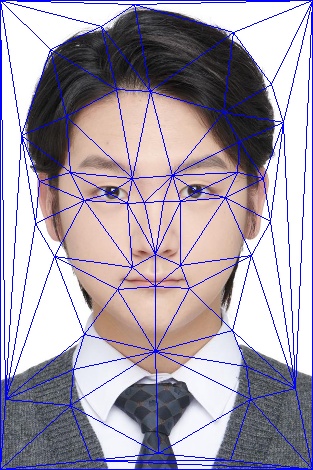
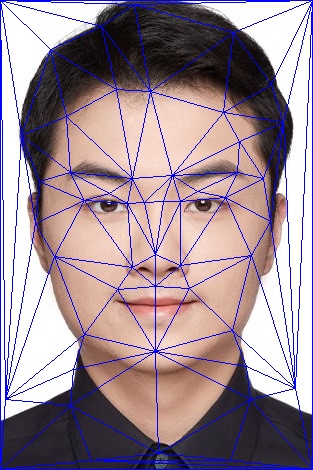
My friend Junye's face with Delaunay triangulation

Part 2: The mid-way face

We now have im1 and im2 as the two images, and the im1_pts and im2_pts as the correspondence point pairs.

Also, we have the Delaunay triangulation of the mean set of points.

We first create the mid-way shape by averaging the x and y coordinates of the correspondence point pairs. Given we have computed the mean_pts in Part 1, this works as the mid-way shape.

Then, we create the mid-way face by warping the two images to the mid-way shape, using the Delaunay triangulation given in Part 1.

Specifically, for every pixel from the original two images, we do an affine transformation to the mid-way shape, and then use the pixel value at the transformed location as the pixel value of the mid-way face.

Part 3: The morph sequence

$[0,1]$ . I equally separate the interval into 31 values, which means the gif output will be 31 fps.

# Part 4: The "Mean face" of a population

We first read the whole dataset of Dane faces, load the images and parse the corresponding points from asf files.

Then, we create a mean shape for the population.

Actually, I choose the mean shape of neutral faces and happy faces, and morphed 3 examples of each subset to the mean respectively.

3 warp example of neutral faces (shape-only)

3 warp example of happy faces (shape-only)

The average face of neutral, happy and all faces in the dataset is shown below:

Also, I create the warp from mean face to me and me to the mean face (shape-only):

It seems not so normal, which can be due to the blurry outline of the Average Dane image.

# Part 5: Caricatures: Extrapolating from the mean

$\alpha$ .

Specifically, we let the shape of the extrapolated face be:

\begin{matrix} shape = source shape + α \times (destination shape - source shape) \\ = (1 - α) \times source shape + α \times destination shape \end{matrix}

and the appearance is kept the same as the source face.

$\alpha > 1$ , we can get the caricature of the source face towards the characteristics of the destination face.

$\alpha = 1.5$ and try caricature towards the mean face of happy Dane faces.

Because I didn't show my teeth when taking this photo, only my mouth lips are stretched. Also because the blurry outline of the average image, the correspondence is more difficult, and also the extrapolated image seems unnatural in the outline.

Part 6: Bells and Whistles

6.1: Gender changing

We can change from my face to a female face by

first compute the mean shape of female faces,
morph my face to the mean via a pair of dissolve and warp fractions.

$[0,1]$ as follows: